machine learningのIntroおよびIntermediateと受講してきて、いよいよ、昨今のAIブームのきっかけともいえるDeep Learingについて学び進めていきたいと思います。そこで、KaggelのCourseにある、Intro to Deep Learningを受講してみることにしました。

A Single Neuron
ここでは、ニューラルネットワークの基本的な概念を学習しました。ニューロンに対して入力xが入れられ、出力としてyが得られます。このyの値が学習データと一致するようにウェイトwとバイアスbが学習されていくのがディープラーニングになります。
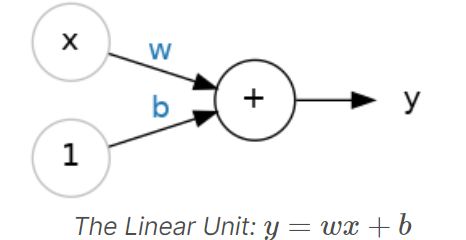
上の図では入力は1系統でしたが、複数の入力があるケースも同様の考えです。
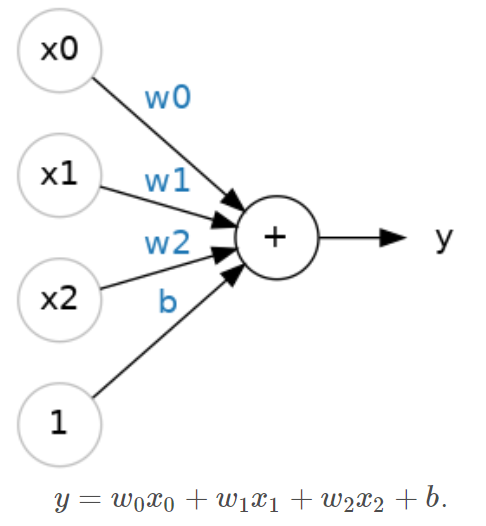
このようなニューラルネットワークを実装するために、PythonではKerasを活用し実装します。

ニューロンの層をlayersとして入れ子にしていくことで実現するようです。この例は上図の3つの入力があり、1つの層、1つのニューロンで処理するコードになります。Denseの引数としてunitsでニューロンの数、input_shapeで入力値の数を指定しています。
Deep Neural Networks
この章では、より複雑なニューラルネットワークの実装方法を学習します。Kerasでは各層をLayersとして積み重ねていくことになります。
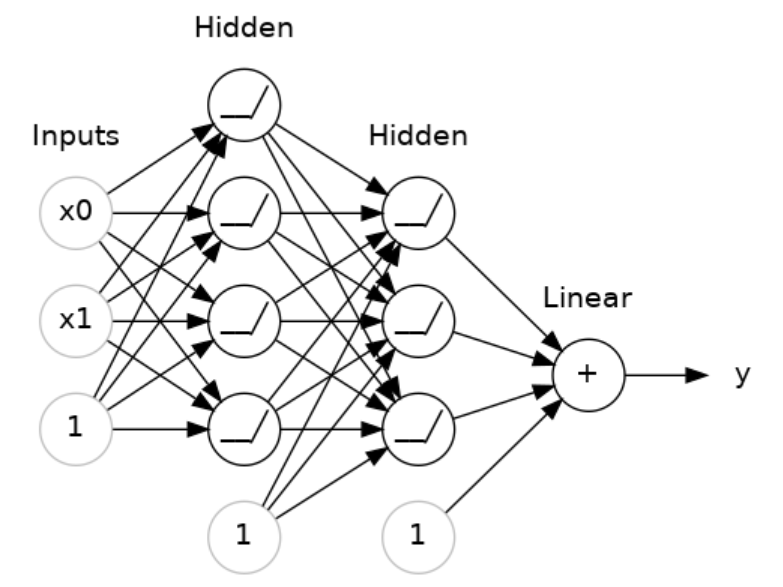
上の図のネットワークを実装するコードが下記となります。複数の層を使用する場合、keras.Sequentialの中に入れ子でlayerを列挙してくことになります。ここで、layers.Denseのactivationにて活性化関数を指定しています(ここではreluを指定)。

なお、活性化関数の指定方法としては、Denseの引数activationとして与える方法以外にも、layerとして対象の層の後にlayers.Activationとして追加することでも実現でき、以下の二つのコードは同じ意味を持つ。


Stochastic Gradient Descent
ここまでで、ニューラルネットワークを実装する方法について学びました。ここで、各ニューロンでの計算に使用されるウェイトの初期値としてはランダムに設定され、学習によりウェイトを調整していくことになります。この章では学習の方法について学びます。
ニューラルネットワークにおける学習では、入力となる複数の特徴量と、期待する出力である教師データのセットが必要となります。
その他にも、推論結果がどれほど適切に推論できているかを測るloss function(損失関数)、学習過程でのウェイトの変更方針を指定するOptimizer(最適化アルゴリズム)も併せて検討する必要があります。
loss function(損失関数)は、モデルの推論結果と正解(教師データ)の差を示す関数です。regression(回帰)問題における有名なloss functionはMAE(Mean Absolute Error:予測値と正解値の差分の絶対値の平均)です。loss functionを指定することでモデルが得べき問題の目的を定義するようです(Loss Functionが最小となるように学習する)。
Optimizer(最適化アルゴリズム)は、学習するため(ウェイトを調整するため)の方法を定義します。ディープラーニングで用いるOptimizerは基本的にSGD(確率的勾配降下法)に分類される手法で、トレーニングデータをモデルに入力し出力と正解の値をチェックし最小化するようウェイトを更新していくこと学習通して繰り返していきます。
これらのLoss FunctionおよびOptimizerはモデルをコンパイルする際に指定します。

その後、batch_sizeで1回の学習のためにモデルに与えるデータの件数を指定し、epochで全学習データを何回繰り返し学習するかを指定して、学習(fit)を実行させます。

Exerciseでは、Learning Rate(学習率)やBatch Sizeを変更して学習にかかる時間や、損失の変化具合を調整する方法を体験し、下記の点を確認できます。
- バッチサイズが小さいほど、損失曲線のノイズが大きくなる。
- 学習率が小さいと、学習が収束するのに時間がかかる。
- 学習率を大きくすると収束は早くなる傾向にあるが収束せず失敗することもある。
Overfitting and Underfitting
kerasでは、学習過程をhistoryとして保持するため、これをグラフ化するなどして確認することにより、過学習や学習不足についての理解を深めます。
学習データは、NoiseとSignalに分類されます。Signalはモデルが推論をするにあたり有用なデータのことであり、逆にNoiseは推論には役に立たず、学習データにのみ依存するデータが該当します。
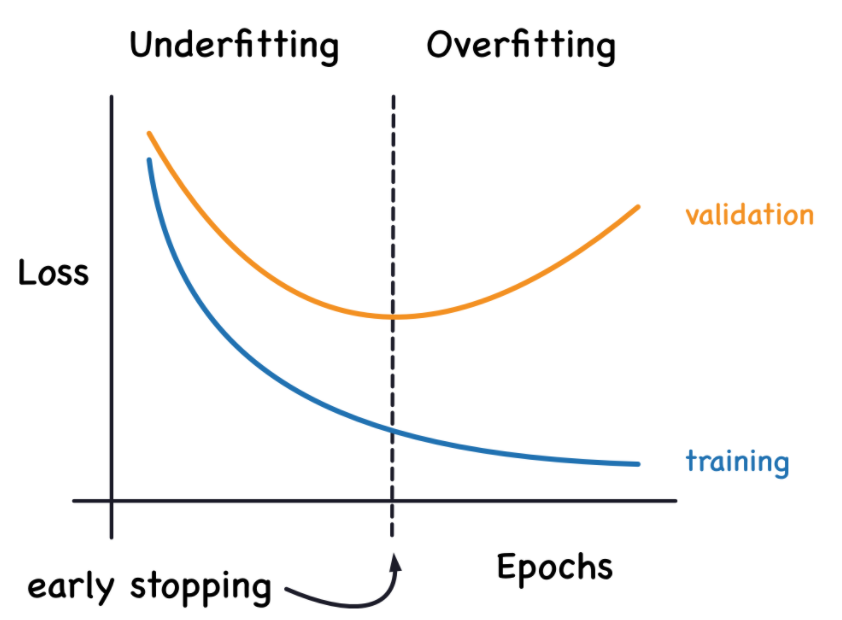
EpochごとにどのようにLossが推移するかを、トレーニングデータを用いたカーブ(青線)と、バリデーション(評価用)データを用いたカーブ(オレンジ線)を併記したLearning Curve(学習曲線)を活用して効率的に学習させる方法を学びます。
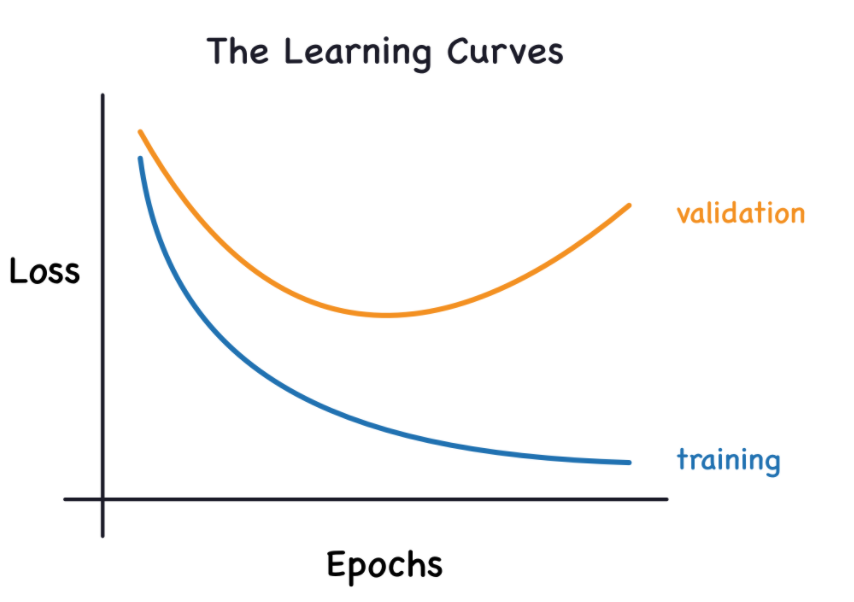
Lossが十分に下がっていない状態をUnderfitting(過少学習、未学習)といいます。またトレーニングデータに対するLossは極めて低いのに、バリデーションデータに対するLossが大きくなっている状態(上手の右端の方)をOverfitting(過学習)といいます。
モデルのCapacity(キャパシティ)は、モデルが学習できるサイズと複雑さを表します。ニューラルネットワークにおいては、そのモデルが持つニューロンの数とそれらの結合のされ方に依存します。モデルがUnderfittingしているようであれば、キャパシティを上げることを検討すべきとのことです。モデルのキャパシティを上げるには、広く(既存のレイヤにニューロンを追加)するか、深く(レイヤを追加)する必要があります。より広いモデルは線形の関係性のあるデータに有効で、より深いモデルは非線形の関係にあるデータに有効なようです。
モデルが余計なノイズまで含めて学習しすぎてしまうOverfittingですが、これの対策としてEarly Stoppingがあります。EpochごとにLossを計算し、Lossが減少している間は学習を行い、Lossが増加したら学習を止めてしまい、Overfittingする前の段階で学習を止めてしまう事です。
Early StoppingはKerasに含まれるtensorflow.keras.callbacks.EarlyStoppingを使用することで実現できます。
Dropout and Batch Normalization
Dense層は、ニューロンを結合させる層でしたが、Deep Learningの世界においては、前処理や変換処理行う層も追加することができます。この章では、前処理、変換処理の例として、Dropout(ドロップアウト)とBatch Normalization(バッチ正則化)の使い方を学びます。
Dropoutは、トレーニングのすべてのステップで、レイヤーのユニットの一部をランダムに削除することで、ネットワークが特定のトレーニングデータに強く依存したパターンを学習しにくくします。
使用するには、Dropoutさせたい層の直前に、引数として「ユニットを削除する割合」を指定してDroput層を挿入してやることになります。

Batch Normalizationまたは、Batchnorm(バッチ正則化)についてですが、こちらは、学習を効果的(早く、安定的に)に行えるようにする手法です。ニューラルネットワークの学習において、大きさの大きく異なる入力データが存在すると、大きい方のデータに引っ張られ学習がうまくいかないことがあるようです。それを防ぐため、Batch Normalizationでは、スケールを合わせるような処理を行うことで、入力データ間での大きさの差を縮めるようにすることで学習を安定化させます。
Batch Normalizationも、層としてBatchNormalizationを追加することで使用することができます。Batch Normalizationも、層としてBatchNormalizationを追加することで使用することができます。

Binary Classification
ここまでは、回帰問題を解く手法を学んできましたが、ここでは分類問題に取り組みます。いままでの回帰問題の解き方と異なるのは、Loss Function(損失関数)と出力層での出力です。
ここでは、Binary Classification(2項分類)について見ていきます。Binary Classificationは、”Yes”か”No”か、”犬”か”猫”か、など2つのどちらに属するかを予測する問題となりますが、まずは、各選択肢に対して”Yes”=0、”No”=1のように数値のラベルを付与することでニューラルネットワークで取り扱います。
分類問題では、Accuracy(正解率)が評価指標として良く用いられますが、これはそのまま損失関数として扱うことができません。代わりにCross-Entropy関数を用いることになります。
また、出力層の値に対しては、0から1の数値に変換するためにシグモイド関数を活性化関数として用います。
したがって、分類に用いるモデルは以下のように定義できます。回帰のコードとほぼ同じですが、最後の出力層の活性化関数としてシグモイドを指定している点が異なります。

また、モデルをコンパイルする際には、lossとして、’binary_crossentropy’、metricsに’binary_accuracy’を指定します。

その他は回帰同様で、keras.callbacks.EarlyStoppingを用いてEarly Stoppingを有効にしたり、Dropout層を使って過学習を抑制したりできます。
まとめ
以上で、Intro to Deep LearningのCourseは終了となります。説明されている事項は少し難しくはなってきていますが、コード自体は簡単に思われます。
ただ、これだけでは実際のCompetitionに参加できる気がしません。。。とりあえず、Intro系のCourseはすべて受けてみようと思うので、次は、Intro to Game AI and Reinforcement Learningを受けてみようと思います。

